单层感知器为什么不能解决异或(XOR)问题
单层感知器为什么不能解决异或问题(XOR)问题?给出两个思路去考虑这个小问题~
最近翻到了自己在印象笔记中学习记录的一些知识点,后续准备系统地整理放在自己的博客上,还请各位不吝指教。
1. 感知器模型
感知器模型是美国学者罗森勃拉特(Frank Rosenblatt)为研究大脑的存储、学习和认知过程而提出的一类具有自学习能力的神经网络模型,它把神经网络的研究从纯理论探讨引向了从工程上的实现。
Rosenblatt提出的感知器模型是一个只有单层计算单元的前向神经网络,称为单层感知器。
2. 单层感知器模型算法概述
在学习基础的NN知识的时候,单个神经元的结构必定是最先提出来的,单层感知器模型算法与神经元结构类似;
大概思想是:首先把连接权和阈值初始化为较小的非零随机数,然后把有n个连接权值的输入送入网络,经加权运算处理,得到的输出如果与所期望的输出有较大的差别(对比神经元模型中的激活函数),就对连接权值参数进行自动调整,经过多次反复,直到所得到的输出与所期望的输出间的差别满足要求为止。
如下为简单起见,仅考虑只有一个输出的简单情况。设$x_i(t)$是时刻$t$感知器的输入(i=1,2,……,n),$ω_i(t)$是相应的连接权值,$y(t)$是实际的输出,$d(t)$是所期望的输出,且感知器的输出或者为1,或者为0。
3. 线性不可分问题
单层感知器不能表达的问题被称为线性不可分问题。 1969年,明斯基证明了“异或”问题是线性不可分问题。
4. “与”、”或”、”非”问题的证明
- 由于单层感知器的输出为:
所以,用感知器实现简单逻辑运算的情况如下:
“与”运算(And, x1∧x2)
令 ω1 = ω2 = 1,θ = 1.5,则: y = f(1 x1 + 1 x2 - 1.5)
显然,当x1和x2均为1时,y的值1;而当x1和x2有一个为0时,y的值就为0.“或”运算(Or, x1∨x2)
令ω1 = ω2=1, θ = 0.5,则: y=f(1 x1 + 1 x2 - 0.5)
显然,只要x1和x2中有一个为1,则y的值就为1;只有当x1和x2都为0时,y的值才为0。“非”运算(Not, ~X1)
令ω1 = -1, ω2 = O, θ = -0.5,则: y = f((-1) x1 + 1 x2 + 0.5)
显然,无论x2为何值,x1为1时,y的值都为0;x1为0时,y的值为1。即y总等于~x1。“异或”运算(x1 XOR x2)
5. “异或”问题的证明
5.1 单层感知机不能解决”异或”问题证明方法一
如果“异或”(XOR)问题能用单层感知器解决,则由XOR的真值映射关系如下:
| (x1, x2) | y |
|---|---|
| (0, 0) | 0 |
| (0, 1) | 1 |
| (1, 0) | 1 |
| (1, 1) | 0 |
则ω1、 ω2 和θ 必须满足如下方程组:
1). ω1 + ω2 - θ < 0 —> θ > ω1 + ω2
2). ω1 + 0 - θ ≥ 0 —> 0 ≥ θ - ω1
3). 0 + 0 - θ < 0 —> θ > 0
4). 0 + ω2 - θ ≥ 0 —> 0 ≥ θ - ω2
显然,该方程组是矛盾的,无解!这就说明单层感知器是无法解决异或问题的。
5.2 单层感知机不能解决”异或”问题证明方法二
首先需要证明以下定理:
样本集线性可分的充分必要条件是正实例点集所构成的凸壳与负实例点集所构成的凸壳互不相交
必要性:假设样本集T线性可分,则存在一个超平面W将数据集正实例点和负实例点完全正确地划分到超平面两侧。显然两侧的点分别构成的凸壳互不相交;
充分性:假设存在两个凸壳A、B相交,且存在超平面W将A和B线性分割,令A在B的凸壳内部的点为a,因为线性可交,则A中不存在两点之间的连线与超平面W相交,而凸壳B中任意一点与A中的点的连线均与超平面W相交,则B内部的点a也与A中任一点之间的连线不与W相交,与B壳中任一点与A中的点的连线均与超平面W相交矛盾。
故:只有正负实例点所构成的两个凸壳不相交时样本集才线性可分。
显然,对于此例,负实例样本集[(0, 0), (1, 1)] 和 正实例样本集[(0, 1), (1, 0)]是二维中是不能被线性分割的。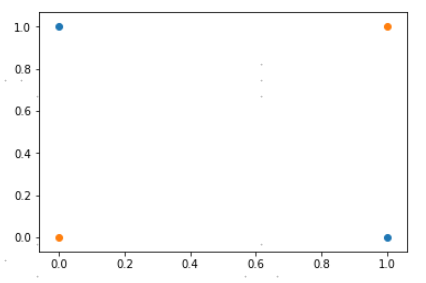
单层感知器为什么不能解决异或(XOR)问题