概率论2-随机过程
随机过程(Stochastic Process) 是一组随机变量$X_t$的集合,其中$t$属于一个索引(index)集合$\cal{T}$。索引集合$\cal{T}$可以定义在时间域或者空间域,但一般为时间域,以实数或正数表示。当t为实数时,随机过程为连续随机过程;当t为整数时,为离散随机过程。
日常生活中的很多例子包括股票的波动、语音信号、身高的变化等都可以看作是随机过程。常见的和时间相关的随机过程模型包括伯努利过程、随机游走(Random Walk)、马尔可夫过程等。和空间相关的随机过程通常称为随机场(Random Field)。比如一张二维的图片,每个像素点(变量)通过空间的位置进行索引,这些像素就组成了一个随机过程。
1. 马尔可夫过程
马尔可夫性质 在随机过程中,马尔可夫性质(Markov Property)是指一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态。以离散随机过程为例,假设随机变量$X_0,X_1, … ,X_T$构成一个随机过程。这些随机变量的所有可能取值的集合被称为状态空间(State Space)。如果$X_{t+1}$对于过去状态的条件概率分布仅是$X_t$的一个函数,则
其中$X{0:t}$表示变量集合$X_0,X_1, … ,X_t,x_{0:t}$表示为在状态空间中的状态序列。
马尔可夫性质也可以描述为给定当前状态时,将来的状态与过去状态是条件独立的。
1.1 马尔可夫链
离散时间的马尔可夫过程也称为马尔可夫链(Markov Chain)。如果一个马尔可夫链的条件概率
在不同时间都是不变的,即和时间$t$无关,则称为时间同质的马尔可夫链(Time-Homogeneous Markov Chains)。如果状态空间是有限的,$T(s_i, s_j)$也可以用一个矩阵$T$表示,称为状态转移矩阵(Transition Matrix),其中元素$t_{ij}$表示状态$s_i$转移到状态$s_j$的概率。
平稳分布 假设状态空间大小为$M$,向量$\pi = [\pi_1, … , 、\pi_M]^T$ 为状态空间中的一个分布,满足$0 ≤ \pi_i ≤ 1$ 和$\sum_{i=1}^{M}\pi_i =1$。
对于状态转移矩阵为$T$的时间同质的马尔可夫链,如果存在一个分布$\pi$满足
即分布$\pi$就称为该马尔可夫链的平稳分布(Stationary Distribution)。根据特征向量的定义可知,$\pi$为矩阵$T$的(归一化)的对应特征值为1的特征向量。
如果一个马尔可夫链的状态转移矩阵T满足所有状态可遍历性以及非周期性,那么对于任意一个初始状态分布$\pi^{(0)}$,将经过一定时间的状态转移之后,都会收敛到平稳分布,即
定理1 - 细致平稳条件(Detailed Balance Condition): 如果一个马尔科夫链满足
则一定会收敛到平稳分布$\pi$。
细致平稳条件保证了从状态$i$转移到状态$j$的数量和从状态$j$转移到状态$i$的数量相一致,相互抵消,所以数量不发生改变。
细致平稳条件只是马尔科夫链收敛的充分条件,不是必要条件。
2. 高斯过程
高斯过程(Gaussian Process)也是一种应用广泛的随机过程模型。假设有一组连续随机变量$X_0,X_1, … ,X_T$ ,如果由这组随机变量构成的任一有限集合$X_{t_1,… ,t_k} = [X_{t_1} , … ,X_{t_n}]^T$都服从一个多元正态分布,那么这组随机变量为一个随机过程。高斯过程也可以定义为:如果$X_{t_1, … ,t_n}$ 的任一线性组合都服从一元正态分布,那么这组随机变量为一个随机过程。
高斯过程回归 高斯过程回归(Gaussian Process Regression)是利用高斯过程来对一个函数分布进行建模。和机器学习中参数化建模(比如贝叶斯线性回归)相比,高斯过程是一种非参数模型,可以拟合一个黑盒函数,并给出拟合结果的置信度[Rasmussen, 2004]。
假设一个未知函数$f(x)$服从高斯过程,且为平滑函数。如果两个样本$x_1, x_2$比较接近,那么对应的$f(x_1), f(x_2)$也比较接近。假设从函数$f(x)$中采样有限个样本$X = [x_1, x_2, … , x_N]$,这$N$个点服从一个多元正态分布,
其中$\mu(X) = [\mu(x_1), \mu(x_2), … , \mu(x_N)]^T$是均值向量,$K(X,X) = [k(x_i, x_j )]_{N×N}$是协方差矩阵,$k(x_i, x_j)$为核函数,可以衡量两个样本的相似度。
在高斯过程回归,一个常用的核函数是平方指数(Squared Exponential)函数
其中$l$为超参数。当$x_i$和$x_j$越接近,其核函数的值越大,表明$f(x_i)$和$f(x_j)$越相关。
假设$f(x)$的一组带噪声的观测值为${(x_n, y_n)}_{n=1}^N$,其中$y_n \sim N(f(x_n), \sigma^2)$为正态分布,$\sigma$为噪声方差。
对于一个新的样本点$x^∗$,我们希望预测函数$y^∗ = f(x^∗)$。令$y = [y_1, y_2, … , y_n]$为已有的观测值,根据高斯过程的假设,$[y; y^∗]$ 满足
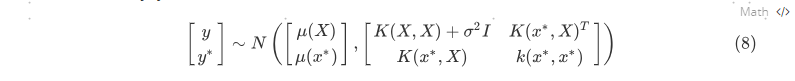
其中$K(x^*,X) = [k(x^∗, x_1), … , k(x^∗, x^n)]$。
根据上面的联合分布,$y^∗$的后验分布为
其中均值$\hat{\mu}$和方差$\hat{\sigma}$为
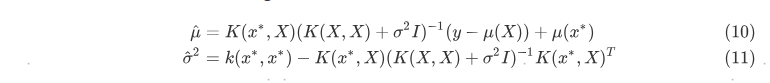
从公式(10) 可以看出,均值函数$\mu(x)$可以近似地互相抵消。在实际应用中,一般假设$\mu(x) = 0$,均值$\hat{\mu}$可以将简化为
高斯过程回归可以认为是一种有效的贝叶斯优化方法,广泛地应用于机器学习中。