深广度搜索手写实现与networkx对比
前面项目在做一个遍历搜索的时候,有用到深度/广度搜索的相关知识;原理很简单,不再拾人牙慧了;这篇文章主要是将我自己简单实现的深广度搜索分享出来并与Python networkx模块中的已有实现做一个简单对比。
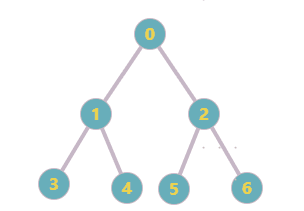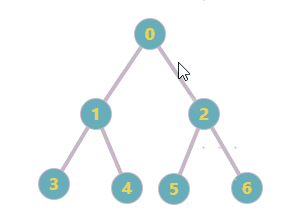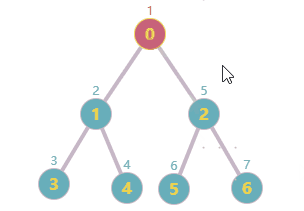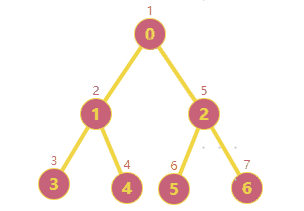
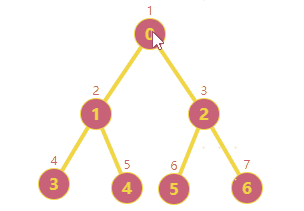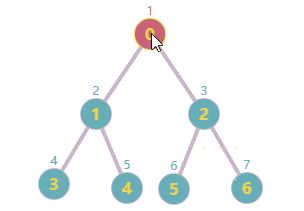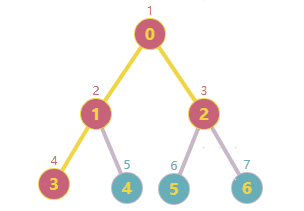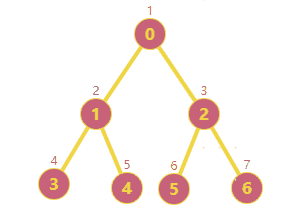
前面项目在做一个遍历搜索的时候,有用到深度/广度搜索的相关知识;原理很简单,不再拾人牙慧了;这篇文章主要是将我自己简单实现的深广度搜索分享出来并与Python networkx模块中的已有实现做一个简单对比。


主要总结了交叉熵、KL散度、JS散度和wasserstein距离(也称推土机距离,EMD)的相关知识,其中EMD的直观表示可以参见下图:

对应分布为$p(x)$的随机变量,熵$H(p)$表示其最优编码长度。交叉熵(Cross Entropy)是按照概率分布$q$的最优编码对真实分布为$p$的信息进行编码的长度,
信息论(Information Theory)是数学、物理、统计、计算机科学等多个学科的交叉领域。信息论是由Claude Shannon 最早提出的,主要研究信息的量化、存储和通信等方法。这里,“信息”是指一组消息的集合。假设在一个噪声通道上发送消息,我们需要考虑如何对每一个信息进行编码、传输以及解码,使得接收者可以尽可能准确地重构出消息。
在机器学习相关领域,信息论也有着大量的应用。比如特征抽取、统计推断、自然语言处理等。
优化问题一般都是通过迭代的方式来求解:通过猜测一个初始的估计$x_0$,然后不断迭代产生新的估计$x_1, x_2, … x_t$,希望$x_t$最终收敛到期望的最优解$x^∗$。
一个好的优化算法应该是在一定的时间或空间复杂度下能够快速准确地找到最优解。同时,好的优化算法受初始猜测点的影响较小,通过迭代能稳定地找到最优解$x^∗$的邻域,然后迅速收敛于$x^∗$。
优化算法中常用的迭代方法有线性搜索和置信域方法等。线性搜索的策略是寻找方向和步长,具体算法有梯度下降法、牛顿法、共轭梯度法等。在文章中也简要介绍过梯度下降的概念,这里为使得整个体系完整故重新记录一下。
数学优化(Mathematical Optimization)问题,也叫最优化问题,是指在一定约束条件下,求解一个目标函数的最大值(或最小值)问题。
数学优化问题的定义为:给定一个目标函数(也叫代价函数)$f : \cal{A} → \Bbb{R}$,寻找一个变量(也叫参数)$x^* \in \cal{D}$,使得对于所有$\cal{D}$中的$x,f(x^∗) ≤ f(x)$(最小化);或者$f(x^∗) \geq f(x)$(最大化),其中$\cal{D}$为变量$x$的约束集,也叫可行域;$\cal{D}$中的变量被称为是可行解。
随机过程(Stochastic Process) 是一组随机变量$X_t$的集合,其中$t$属于一个索引(index)集合$\cal{T}$。索引集合$\cal{T}$可以定义在时间域或者空间域,但一般为时间域,以实数或正数表示。当t为实数时,随机过程为连续随机过程;当t为整数时,为离散随机过程。
日常生活中的很多例子包括股票的波动、语音信号、身高的变化等都可以看作是随机过程。常见的和时间相关的随机过程模型包括伯努利过程、随机游走(Random Walk)、马尔可夫过程等。和空间相关的随机过程通常称为随机场(Random Field)。比如一张二维的图片,每个像素点(变量)通过空间的位置进行索引,这些像素就组成了一个随机过程。
主要回顾概率论中关于样本空间、随机事件和常见概率分布的基础知识。
样本空间 是一个随机试验所有可能结果的集合。例如,如果抛掷一枚硬币,那么样本空间就是集合{正面,反面}。如果投掷一个骰子,那么样本空间就是{1, 2, 3, 4, 5, 6}。随机试验中的每个可能结果称为样本点。
有些试验有两个或多个可能的样本空间。例如,从52 张扑克牌中随机抽出一张,样本空间可以是数字(A到K),也可以是花色(黑桃,红桃,梅花,方块)。如果要完整地描述一张牌,就需要同时给出数字和花色,这时样本空间可以通过构建上述两个样本空间的笛卡儿乘积来得到。
在实际项目中,对超大矩阵进行计算或者对超大的DataFrame进行计算是一个经常会出现的场景。这里先不考虑开发机本身内存等客观硬件因素,仅从设计上讨论一下不同实现方式带来的性能差异,抛砖引玉。